15 Unsupervised learning
All algorithms presented in Chapters 5 to 9 belong to the larger class of supervised learning tools. Such tools seek to unveil a mapping between predictors \(\textbf{X}\) and a label \(\textbf{Z}\). The supervision comes from the fact that it is asked that the data tries to explain this particular variable \(\textbf{Z}\). Another important part of machine learning consists of unsupervised tasks, that is, when \(\textbf{Z}\) is not specified and the algorithm tries to make sense of \(\textbf{X}\) on its own. Often, relationships between the components of \(\textbf{X}\) are identified. This field is much too vast to be summarized in one book, let alone one chapter. The purpose here is to briefly explain in what ways unsupervised learning can be used, especially in the data pre-processing phase.
15.1 The problem with correlated predictors
Often, it is tempting to supply all predictors to a ML-fueled predictive engine. That may not be a good idea when some predictors are highly correlated. To illustrate this, the simplest example is a regression on two variables with zero mean and covariance and precisions matrices: \[\boldsymbol{\Sigma}=\textbf{X}'\textbf{X}=\begin{bmatrix} 1 & \rho \\ \rho & 1 \end{bmatrix}, \quad \boldsymbol{\Sigma}^{-1}=\frac{1}{1-\rho^2}\begin{bmatrix} 1 & -\rho \\ -\rho & 1 \end{bmatrix}.\] When the covariance/correlation \(\rho\) increase towards 1 (the two variables are co-linear), the scaling denominator in \(\boldsymbol{\Sigma}^{-1}\) goes to zero and the formula \(\hat{\boldsymbol{\beta}}=\boldsymbol{\Sigma}^{-1}\textbf{X}'\textbf{Z}\) implies that one coefficient will be highly positive and one highly negative. The regression creates a spurious arbitrage between the two variables. Of course, this is very inefficient and yields disastrous results out-of-sample.
We illustrate what happens when many variables are used in the regression below (Table 15.1). One elucidation of the aforementioned phenomenon comes from the variables Mkt_Cap_12M_Usd and Mkt_Cap_6M_Usd, which have a correlation of 99.6% in the training sample. Both are singled out as highly significant but their signs are contradictory. Moreover, the magnitude of their coefficients are very close (0.21 versus 0.18) so that their net effect cancels out. Naturally, providing the regression with only one of these two inputs would have been wiser.
library(broom) # Package for clean regression output
training_sample %>%
dplyr::select(c(features, "R1M_Usd")) %>% # List of variables
lm(R1M_Usd ~ . , data = .) %>% # Model: predict R1M_Usd
tidy() %>% # Put output in clean format
filter(abs(statistic) > 3) %>% # Keep significant predictors only
knitr::kable(booktabs = TRUE,
caption = "Significant predictors in the training sample.") | term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 0.0405741 | 0.0053427 | 7.594323 | 0.0000000 |
| Ebitda_Margin | 0.0132374 | 0.0034927 | 3.789999 | 0.0001507 |
| Ev_Ebitda | 0.0068144 | 0.0022563 | 3.020213 | 0.0025263 |
| Fa_Ci | 0.0072308 | 0.0023465 | 3.081471 | 0.0020601 |
| Fcf_Bv | 0.0250538 | 0.0051314 | 4.882465 | 0.0000010 |
| Fcf_Yld | -0.0158930 | 0.0037359 | -4.254126 | 0.0000210 |
| Mkt_Cap_12M_Usd | 0.2047383 | 0.0274320 | 7.463476 | 0.0000000 |
| Mkt_Cap_6M_Usd | -0.1797795 | 0.0459390 | -3.913443 | 0.0000910 |
| Mom_5M_Usd | -0.0186690 | 0.0044313 | -4.212972 | 0.0000252 |
| Mom_Sharp_11M_Usd | 0.0178174 | 0.0046948 | 3.795131 | 0.0001476 |
| Ni | 0.0154609 | 0.0044966 | 3.438361 | 0.0005854 |
| Ni_Avail_Margin | 0.0118135 | 0.0038614 | 3.059359 | 0.0022184 |
| Ocf_Bv | -0.0198113 | 0.0052939 | -3.742277 | 0.0001824 |
| Pb | -0.0178971 | 0.0031285 | -5.720637 | 0.0000000 |
| Pe | -0.0089908 | 0.0023539 | -3.819565 | 0.0001337 |
| Sales_Ps | -0.0157856 | 0.0046278 | -3.411062 | 0.0006472 |
| Vol1Y_Usd | 0.0114250 | 0.0027923 | 4.091628 | 0.0000429 |
| Vol3Y_Usd | 0.0084587 | 0.0027952 | 3.026169 | 0.0024771 |
In fact, there are several indicators for the market capitalization and maybe only one would suffice, but it is not obvious to tell which one is the best choice.
To further depict correlation issues, we compute the correlation matrix of the predictors below (on the training sample). Because of its dimension, we show it graphically. As there are too many labels, we remove them.
library(corrplot) # Package for plots of correlation matrices
C <- cor(training_sample %>% dplyr::select(features)) # Correlation matrix
corrplot(C, tl.pos='n') # Plot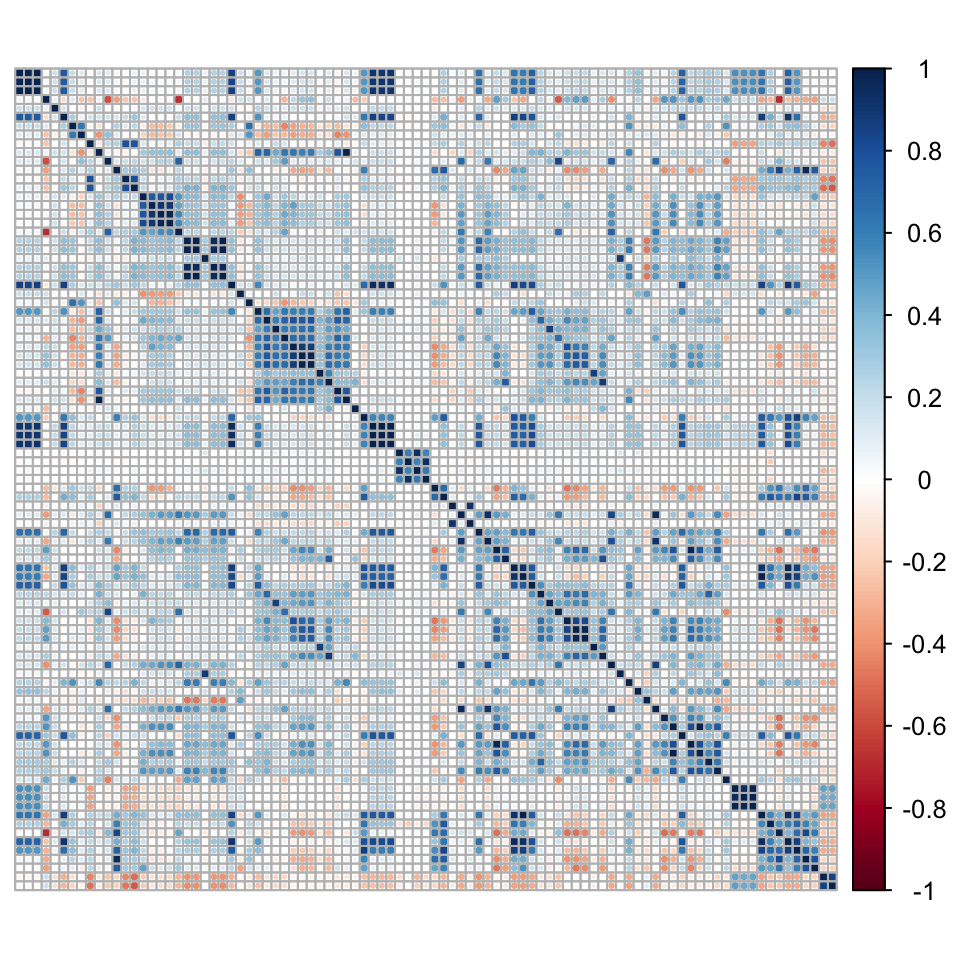
FIGURE 15.1: Correlation matrix of predictors.
The graph of Figure 15.1 reveals several blue squares around the diagonal. For instance, the biggest square around the first third of features relates to all accounting ratios based on free cash flows. Because of this common term in their calculation, the features are naturally highly correlated. These local correlation patterns occur several times in the dataset and explain why it is not a good idea to use simple regression with this set of features.
In full disclosure, multicollinearity (when predictors are correlated) can be much less a problem for ML tools than it is for pure statistical inference. In statistics, one central goal is to study the properties of \(\beta\) coefficients. Collinearity perturbs this kind of analysis. In machine learning, the aim is to maximize out-of-sample accuracy. If having many predictors can be helpful, then so be it. One simple example can help clarify this matter. When building a regression tree, having many predictors will give more options for the splits. If the features make sense, then they can be useful. The same reasoning applies to random forests and boosted trees. What does matter is that the large spectrum of features helps improve the generalization ability of the model. Their collinearity is irrelevant.
In the remainder of the chapter, we present two approaches that help reduce the number of predictors:
- the first one aims at creating new variables that are uncorrelated with each other. Low correlation is favorable from an algorithmic point of view, but the new variables lack interpretability;
- the second one gathers predictors into homogeneous clusters and only one feature should be chosen out of this cluster. Here the rationale is reversed: interpretability is favored over statistical properties because the resulting set of features may still include high correlations, albeit to a lesser point compared to the original one.
15.2 Principal component analysis and autoencoders
The first method is a cornerstone in dimensionality reduction. It seeks to determine a smaller number of factors (\(K'<K\)) such that:
- i) the level of explanatory power remains as high as possible;
- ii) the resulting factors are linear combinations of the original variables;
- iii) the resulting factors are orthogonal.
15.2.1 A bit of algebra
In this short subsection, we define some key concepts that are required to fully understand the derivation of principal component analysis (PCA). Henceforth, we work with matrices (in bold fonts). An \(I \times K\) matrix \(\textbf{X}\) is orthonormal if \(I> K\) and \(\textbf{X}'\textbf{X}=\textbf{I}_K\). When \(I=K\), the (square) matrix is called orthogonal and \(\textbf{X}'\textbf{X}=\textbf{X}\textbf{X}'=\textbf{I}_K\), i.e., \(\textbf{X}^{-1}=\textbf{X}'\).
One foundational result in matrix theory is the Singular Value Decomposition (SVD, see, e.g., chapter 5 in Meyer (2000)). The SVD is formulated as follows: any \(I \times K\) matrix \(\textbf{X}\) can be decomposed into \[\begin{equation} \tag{15.1} \textbf{X}=\textbf{U} \boldsymbol{\Delta} \textbf{V}', \end{equation}\] where \(\textbf{U}\) (\(I\times I\)) and \(\textbf{V}\) (\(K \times K\)) are orthogonal and \(\boldsymbol{\Delta}\) (with dimensions \(I\times K\)) is diagonal, i.e., \(\Delta_{i,k}=0\) whenever \(i\neq k\). In addition, \(\Delta_{i,i}\ge 0\): the diagonal terms of \(\boldsymbol{\Delta}\) are nonnegative.
For simplicity, we assume below that \(\textbf{1}_I'\textbf{X}=\textbf{0}_K'\), i.e., that all columns have zero sum (and hence zero mean).32 This allows to write that the covariance matrix is equal to its sample estimate \(\boldsymbol{\Sigma}_X= \frac{1}{I-1}\textbf{X}'\textbf{X}\).
One crucial feature of covariance matrices is their symmetry. Indeed, real-valued symmetric (square) matrices enjoy a SVD which is much more powerful: when \(\textbf{X}\) is symmetric, there exist an orthogonal matrix \(\textbf{Q}\) and a diagonal matrix \(\textbf{D}\) such that \[\begin{equation} \tag{15.2} \textbf{X}=\textbf{Q}\textbf{DQ}'. \end{equation}\] This process is called diagonalization (see chapter 7 in Meyer (2000)) and conveniently applies to covariance matrices.
15.2.2 PCA
The goal of PCA is to build a dataset \(\tilde{\textbf{X}}\) that has fewer columns but that keeps as much information as possible when compressing the original one, \(\textbf{X}\). The key notion is the change of base, which is a linear transformation of \(\textbf{X}\) into \(\textbf{Z}\), a matrix with identical dimension, via \[\begin{equation} \tag{15.3} \textbf{Z}=\textbf{XP}, \end{equation}\] where \(\textbf{P}\) is a \(K \times K\) matrix. There are of course an infinite number of ways to transform \(\textbf{X}\) into \(\textbf{Z}\), but two fundamental constraints help reduce the possibilities. The first constraint is that the columns of \(\textbf{Z}\) be uncorrelated. Having uncorrelated features is desirable because they then all tell different stories and have zero redundancy. The second constraint is that the variance of the columns of \(\textbf{Z}\) is highly concentrated. This means that a few factors (columns) will capture most of the explanatory power (signal), while most (the others) will consist predominantly of noise. All of this is coded in the covariance matrix of \(\textbf{Z}\):
- the first condition imposes that the covariance matrix be diagonal;
- the second condition imposes that the diagonal elements, when ranked in decreasing magnitude, see their value decline (sharply if possible).
The covariance matrix of \(\textbf{Z}\) is \[\begin{equation} \tag{15.4} \boldsymbol{\Sigma}_Z=\frac{1}{I-1}\textbf{Z}'\textbf{Z}=\frac{1}{I-1}\textbf{P}'\textbf{X}'\textbf{XP}=\frac{1}{I-1}\textbf{P}'\boldsymbol{\Sigma}_X\textbf{P}. \end{equation}\]
In this expression, we plug the decomposition (15.2) of \(\boldsymbol{\Sigma}_X\): \[\boldsymbol{\Sigma}_Z=\frac{1}{I-1}\textbf{P}'\textbf{Q}\textbf{DQ}'\textbf{P},\] thus picking \(\textbf{P}=\textbf{Q}\), we get, by orthogonality, \(\boldsymbol{\Sigma}_Z=\frac{1}{I-1}\textbf{D}\), that is, a diagonal covariance matrix for \(\textbf{Z}\). The columns of \(\textbf{Z}\) can then be re-shuffled in decreasing order of variance so that the diagonal elements of \(\boldsymbol{\Sigma}_Z\) progressively shrink. This is useful because it helps locate the factors with most informational content (the first factors). In the limit, a constant vector (with zero variance) carries no signal.
The matrix \(\textbf{Z}\) is a linear transformation of \(\textbf{X}\), thus, it is expected to carry the same information, even though this information is coded differently. Since the columns are ordered according to their relative importance, it is simple to omit some of them. The new set of features \(\tilde{\textbf{X}}\) consists in the first \(K'\) (with \(K'<K\)) columns of \(\textbf{Z}\).
Below, we show how to perform PCA and visualize the output with the factoextra package. To ease readability, we use the smaller sample with few predictors.
pca <- training_sample %>%
dplyr::select(features_short) %>% # Smaller number of predictors
prcomp() # Performs PCA
pca # Show the result## Standard deviations (1, .., p=7):
## [1] 0.4536601 0.3344080 0.2994393 0.2452000 0.2352087 0.2010782 0.1140988
##
## Rotation (n x k) = (7 x 7):
## PC1 PC2 PC3 PC4 PC5 PC6
## Div_Yld 0.27159946 -0.57909866 0.04572501 -0.52895604 -0.22662581 -0.506566090
## Eps 0.42040708 -0.15008243 -0.02476659 0.33737265 0.77137719 -0.301883295
## Mkt_Cap_12M_Usd 0.52386846 0.34323935 0.17228893 0.06249528 -0.25278113 -0.002987057
## Mom_11M_Usd 0.04723846 0.05771359 -0.89715955 0.24101481 -0.25055884 -0.258476580
## Ocf 0.53294744 0.19588990 0.18503939 0.23437100 -0.35759553 -0.049015486
## Pb 0.15241340 0.58080620 -0.22104807 -0.68213576 0.30866476 -0.038674594
## Vol1Y_Usd -0.40688963 0.38113933 0.28216181 0.15541056 -0.06157461 -0.762587677
## PC7
## Div_Yld 0.032011635
## Eps 0.011965041
## Mkt_Cap_12M_Usd 0.714319417
## Mom_11M_Usd 0.043178747
## Ocf -0.676866120
## Pb -0.168799297
## Vol1Y_Usd 0.008632062The rotation gives the matrix \(\textbf{P}\): it’s the tool that changes the base. The first row of the output indicates the standard deviation of each new factor (column). Each factor is indicated via a PC index (principal component). Often, the first PC (first column PC1 in the output) loads positively on all initial features: a convex weighted average of all predictors is expected to carry a lot of information. In the above example, it is almost the case, with the exception of volatility, which has a negative coefficient in the first PC. The second PC is an arbitrage between price-to-book (long) and dividend yield (short). The third PC is contrarian, as it loads heavily and negatively on momentum. Not all principal components are easy to interpret.
Sometimes, it can be useful to visualize the way the principal components are built. In Figure 15.2, we show one popular representation that is used for two factors (usually the first two).
library(factoextra) # Package for PCA visualization
fviz_pca_var(pca, # Source of PCA decomposition
col.var="contrib",
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE # Avoid text overlapping
)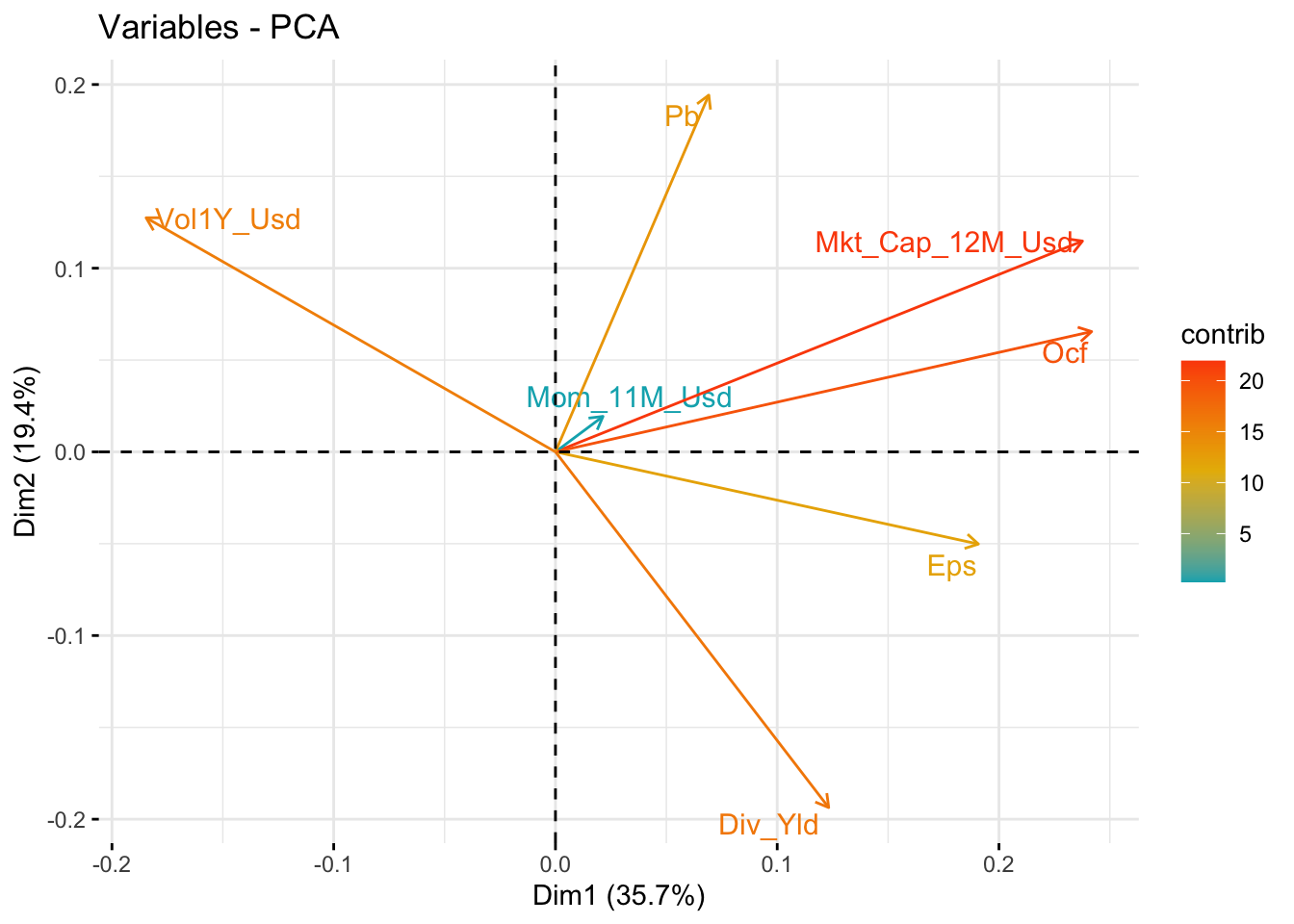
FIGURE 15.2: Visual representation of PCA with two dimensions.
The plot shows that no initial factor has negative signs for the first two principal components. Volatility is negative for the first one and earnings per share and dividend yield are negative for the second. The numbers indicated along the axes are the proportion of explained variance of each PC. Compared to the figures in the first line of the output, the numbers are squared and then divided by the total sum of squares.
Once the rotation is known, it is possible to select a subsample of the transformed data. From the original 7 features, it is easy to pick just 4.
training_sample %>% # Start from large sample
dplyr::select(features_short) %>% # Keep only 7 features
as.matrix() %>% # Transform in matrix
multiply_by_matrix(pca$rotation[,1:4]) %>% # Rotate via PCA (first 4 columns of P)
`colnames<-`(c("PC1", "PC2", "PC3", "PC4")) %>% # Change column names
head() # Show first 6 lines## PC1 PC2 PC3 PC4
## [1,] 0.3989674 0.7578132 -0.13915223 0.3132578
## [2,] 0.4284697 0.7587274 -0.40164338 0.3745255
## [3,] 0.5215295 0.5679119 -0.10533870 0.2574949
## [4,] 0.5445359 0.5335619 -0.08833864 0.2281793
## [5,] 0.5672644 0.5339749 -0.06092424 0.2320938
## [6,] 0.5871306 0.6420126 -0.44566482 0.3075399These 4 factors can then be used as orthogonal features in any ML engine. The fact that the features are uncorrelated is undoubtedly an asset. But the price of this convenience is high: the features are no longer immediately interpretable. De-correlating the predictors adds yet another layer of “blackbox-ing” in the algorithm.
PCA can also be used to estimate factor models. In Equation (15.3), it suffices to replace \(\textbf{Z}\) with returns, \(\textbf{X}\) with factor values and \(\textbf{P}\) with factor loadings (see, e.g., Connor and Korajczyk (1988) for an early reference). More recently, Lettau and Pelger (2020a) and Lettau and Pelger (2020b) propose a thorough analysis of PCA estimation techniques. They notably argue that first moments of returns are important and should be included in the objective function, alongside the optimization on the second moments.
We end this subsection with a technical note. Usually, PCA is performed on the covariance matrix of returns. Sometimes, it may be preferable to decompose the correlation matrix. The result may adjust substantially if the variables have very different variances (which is not really the case in the equity space). If the investment universe encompasses several asset classes, then a correlation-based PCA will reduce the importance of the most volatile class. In this case, it is as if all returns are scaled by their respective volatilities.
15.2.3 Autoencoders
In a PCA, the coding from \(\textbf{X}\) to \(\textbf{Z}\) is straightfoward, linear and works both ways: \[\textbf{Z}=\textbf{X}\textbf{P} \quad \text{and} \quad \textbf{X}=\textbf{ZP}',\] so that we recover \(\textbf{X}\) from \(\textbf{Z}\). This can be writen differently: \[\begin{equation} \tag{15.5} \textbf{X} \quad \overset{\text{encode via }\textbf{P}}{\longrightarrow} \quad \textbf{Z} \quad \overset{\text{decode via } \textbf{P}'}{\longrightarrow} \quad \textbf{X} \end{equation}\]
If we take the truncated version and seek a smaller output (with only \(K'\) columns), this gives:
\[\begin{equation} \tag{15.6} \textbf{X}, \ (I\times K) \quad \overset{\text{encode via }\textbf{P}_{K'}}{\longrightarrow} \quad \tilde{\textbf{X}}, \ (I \times K') \quad \overset{\text{decode via } \textbf{P}'_{K'}}{\longrightarrow} \quad \breve{\textbf{X}},\ (I \times K), \end{equation}\]
where \(\textbf{P}_{K'}\) is the restriction of \(\textbf{P}\) to the \(K'\) columns that correspond to the factors with the largest variances. The dimensions of matrices are indicated inside the brackets. In this case, the recoding cannot recover \(\textbf{X}\) exactly but only an approximation, which we write \(\breve{\textbf{X}}\). This approximation is coded with less information, hence this new data \(\breve{\textbf{X}}\) is compressed and provides a parsimonious representation of the original sample \(\textbf{X}\).
An autoencodeur generalizes this concept to nonlinear coding functions. Simple linear autoencoders are linked to latent factor models (see Proposition 1 in Gu, Kelly, and Xiu (2020a) for the case of single layer autoencoders.) The scheme is the following \[\begin{equation} \tag{15.7} \textbf{X},\ (I\times K) \quad \overset{\text{encode via } N} {\longrightarrow} \quad \tilde{\textbf{X}}=N(\textbf{X}), \ (I \times K') \quad \overset{\text{decode via } N'}{\longrightarrow} \quad \breve{\textbf{X}}=N'(\tilde{\textbf{X}}), \ (I \times K), \end{equation}\]
where the encoding and decoding functions \(N\) and \(N'\) are often taken to be neural networks. The term autoencoder comes from the fact that the target output, which we often write \(\textbf{Z}\) is the original sample \(\textbf{X}\). Thus, the algorithm seeks to determine the function \(N\) that minimizes the distance (to be defined) between \(\textbf{X}\) and the output value \(\breve{\textbf{X}}\). The encoder generates an alternative representation of \(\textbf{X}\), whereas the decoder tries to recode it back to its original values. Naturally, the intermediate (coded) version \(\tilde{\textbf{X}}\) is targeted to have a smaller dimension compared to \(\textbf{X}\).
15.2.4 Application
Autoencoders are easy to code in Keras (see Chapter 7 for more details on Keras). To underline the power of the framework, we resort to another way of coding a NN: the so-called functional API. For simplicity, we work with the small number of predictors (7). The structure of the network consists of two symmetric networks with only one intermediate layer containing 32 units. The activation function is sigmoid; this makes sense since the input has values in the unit interval.
input_layer <- layer_input(shape = c(7)) # features_short has 7 columns
encoder <- input_layer %>% # First, encode
layer_dense(units = 32, activation = "sigmoid") %>%
layer_dense(units = 4) # 4 dimensions for the output layer (same as PCA example)
decoder <- encoder %>% # Then, from encoder, decode
layer_dense(units = 32, activation = "sigmoid") %>%
layer_dense(units = 7) # the original sample has 7 featuresIn the training part, we optimize the MSE and use an Adam update of the weights (see Section 7.2.3).
ae_model <- keras_model(inputs = input_layer, outputs = decoder) # Builds the model
ae_model %>% compile( # Learning parameters
loss = 'mean_squared_error',
optimizer = 'adam',
metrics = c('mean_absolute_error')
)Finally, we are ready to train the data onto itself! The evolution of loss on the training and testing samples is depicted in Figure 15.3. The decreasing pattern shows the progress of the quality in compression.
fit_ae <- ae_model %>%
fit(training_sample %>% dplyr::select(features_short) %>% as.matrix(), # Input
training_sample %>% dplyr::select(features_short) %>% as.matrix(), # Output
epochs = 15, batch_size = 512,
validation_data = list(testing_sample %>% dplyr::select(features_short) %>% as.matrix(),
testing_sample %>% dplyr::select(features_short) %>% as.matrix())
)
plot(fit_ae) + theme_minimal()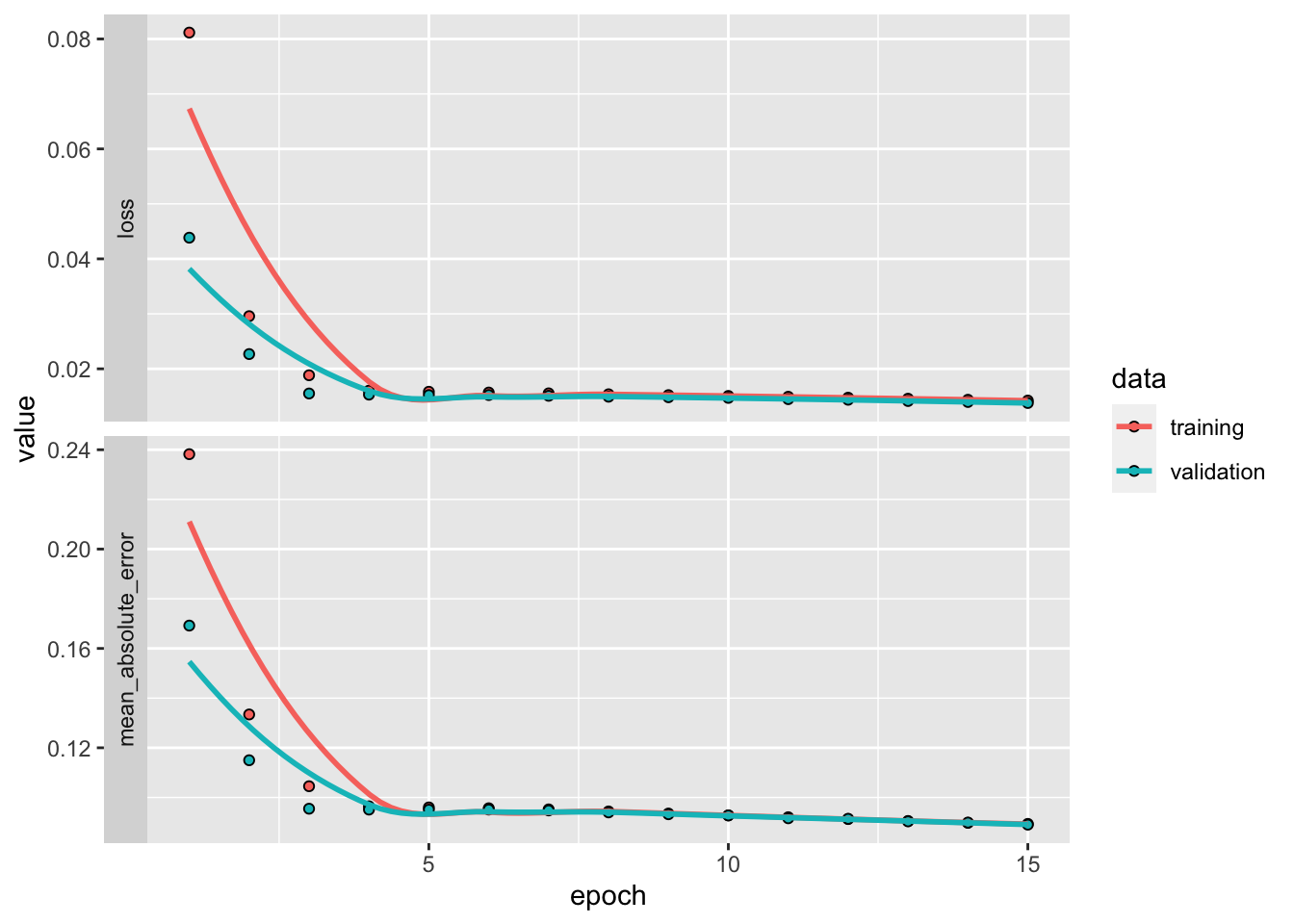
FIGURE 15.3: Output from the training of an autoencoder.
In order to get the details of all weights and biases, the syntax is the following.
ae_weights <- ae_model %>% get_weights()Retrieving the encoder and processing the data into the compressed format is just a matter of matrix manipulation. In practice, it is possible to build a submodel by loading the weights from the encoder (see exercise below).
15.3 Clustering via k-means
The second family of unsupervised tools pertains to clustering. Features are grouped into homogeneous families of predictors. It is then possible to single out one among the group (or to create a synthetic average of all of them). Mechanically, the number of predictors is reduced.
The principle is simple: among a group of variables (the reasoning would be the same for observations in the other dimension) \(\textbf{x}_{\{1 \le j \le J\}}\), find the combination of \(k<J\) groups that minimize \[\begin{equation} \tag{15.8} \sum_{i=1}^k\sum_{\textbf{x}\in S_i}||\textbf{x}-\textbf{m}_i||^2, \end{equation}\] where \(||\cdot ||\) is some norm which is usually taken to be the Euclidean \(l^2\)-norm. The \(S_i\) are the groups and the minimization is run on the whole set of groups \(\textbf{S}\). The \(\textbf{m}_i\) are the group means (also called centroids or barycenters): \(\textbf{m}_i=(\text{card}(S_i))^{-1}\sum_{\textbf{x}\in S_i}\textbf{x}\).
In order to ensure optimality, all possible arrangements must be tested, which is prohibitively long when \(k\) and \(J\) are large. Therefore, the problem is usually solved with greedy algorithms that seek (and find) solutions that are not optimal but ‘good enough’.
One heuristic way to proceed is the following:
- Start with a (possibly random) partition of \(k\) clusters.
- For each cluster, compute the optimal mean values \(\textbf{m}_i^*\) that minimizes expression (15.8). This is a simple quadratic program.
- Given the optimal centers \(\textbf{m}_i^*\), reassign the points \(\textbf{x}_i\) so that they are all the closest to their center.
- Repeat steps 1. and 2. until the points do not change cluster at step 2.
Below, we illustrate this process with an example. From all 93 features, we build 10 clusters.
set.seed(42) # Setting the random seed (the optim. is random)
k_means <- training_sample %>% # Performs the k-means clustering
dplyr::select(features) %>%
as.matrix() %>%
t() %>%
kmeans(10)
clusters <- tibble(factor = names(k_means$cluster), # Organize the cluster data
cluster = k_means$cluster) %>%
arrange(cluster)
clusters %>% filter(cluster == 4) # Shows one particular group## # A tibble: 4 × 2
## factor cluster
## <chr> <int>
## 1 Asset_Turnover 4
## 2 Bb_Yld 4
## 3 Recurring_Earning_Total_Assets 4
## 4 Sales_Ps 4We single out the fourth cluster which is composed mainly of accounting ratios related to the profitability of firms. Given these 10 clusters, we can build a much smaller group of features that can then be fed to the predictive engines described in Chapters 5 to 9. The representative of a cluster can be the member that is closest to the center, or simply the center itself. This pre-processing step can nonetheless cause problems in the forecasting phase. Typically, it requires that the training data be also clustered. The extension to the testing data is not straightforward (the clusters may not be the same).
15.4 Nearest neighbors
To the best of our knowledge, nearest neighbors are not used in large-scale portfolio choice applications. The reason is simple: computational cost. Nonetheless, the concept of neighbors is widespread in unsupervised learning and can be used locally in complement to interpretability tools. Theoretical results on k-NN relating to bounds for error rates on classification tasks can be found in section 6.2 of Ripley (2007). The rationale is the following. If:
- the training sample is able to accurately span the distribution of \((\textbf{y}, \textbf{X})\); and
- the testing sample follows the same distribution as the training sample (or close enough);
then the neighborhood of one instance \(\textbf{x}_i\) from the testing features computed on the training sample will yield valuable information on \(y_i\).
In what follows, we thus seek to find neighbors of one particular instance \(\textbf{x}_i\) (a \(K\)-dimensional row vector). Note that there is a major difference with the previous section: the clustering is intended at the observation level (row) and not at the predictor level (column).
Given a dataset with the same (corresponding) columns \(\textbf{X}_{i,k}\), the neighbors are defined via a similarity measure (or distance) \[\begin{equation} \tag{15.9} D(\textbf{x}_j,\textbf{x}_i)=\sum_{k=1}^Kc_k d_k(x_{j,k},x_{i,k}), \end{equation}\] where the distance functions \(d_k\) can operate on various data types (numerical, categorical, etc.). For numerical values, \(d_k(x_{j,k},x_{i,k})=(x_{j,k}-x_{i,k})^2\) or \(d_k(x_{j,k},x_{i,k})=|x_{j,k}-x_{i,k}|\). For categorical values, we refer to the exhaustive survey by Boriah, Chandola, and Kumar (2008) which lists 14 possible measures. Finally the \(c_k\) in Equation (15.9) allow some flexbility by weighting features. This is useful because both raw values (\(x_{i,k}\) versus \(x_{i,k'}\)) or measure outputs (\(d_k\) versus \(d_{k'}\)) can have different scales.
Once the distances are computed over the whole sample, they are ranked using indices \(l_1^i, \dots, l_I^i\): \[D\left(\textbf{x}_{l_1^i},\textbf{x}_i\right) \le D\left(\textbf{x}_{l_2^i},\textbf{x}_i\right) \le \dots, \le D\left(\textbf{x}_{l_I^i},\textbf{x}_i\right)\]
The nearest neighbors are those indexed by \(l_m^i\) for \(m=1,\dots,k\). We leave out the case when there are problematic equalities of the type \(D\left(\textbf{x}_{l_m^i},\textbf{x}_i\right)=D\left(\textbf{x}_{l_{m+1}^i},\textbf{x}_i\right)\) for the sake of simplicity and because they rarely occur in practice as long as there are sufficiently many numerical predictors.
Given these neighbors, it is now possible to build a prediction for the label side \(y_i\). The rationale is straightforward: if \(\textbf{x}_i\) is close to other instances \(\textbf{x}_j\), then the label value \(y_i\) should also be close to \(y_j\) (under the assumption that the features carry some predictive information over the label \(y\)).
An intuitive prediction for \(y_i\) is the following weighted average: \[\hat{y}_i=\frac{\sum_{j\neq i} h(D(\textbf{x}_j,\textbf{x}_i)) y_j}{\sum_{j\neq i} h(D(\textbf{x}_j,\textbf{x}_i))},\] where \(h\) is a decreasing function. Thus, the further \(\textbf{x}_j\) is from \(\textbf{x}_i\), the smaller the weight in the average. A typical choice for \(h\) is \(h(z)=e^{-az}\) for some parameter \(a>0\) that determines how penalizing the distance \(D(\textbf{x}_j,\textbf{x}_i)\) is. Of course, the average can be taken in the set of \(k\) nearest neighbors, in which case the \(h\) is equal to zero beyond a particular distance threshold: \[\hat{y}_i=\frac{\sum_{j \text{ neighbor}} h(D(\textbf{x}_j,\textbf{x}_i)) y_j}{\sum_{j \text{ neighbor}} h(D(\textbf{x}_j,\textbf{x}_i))}.\]
A more agnostic rule is to take \(h:=1\) over the set of neighbors and in this case, all neighbors have the same weight (see the old discussion by T. Bailey and Jain (1978) in the case of classification). For classification tasks, the procedure involves a voting rule whereby the class with the most votes wins the contest, with possible tie-breaking methods. The interested reader can have a look at the short survey in Bhatia et al. (2010).
For the choice of optimal \(k\), several complicated techniques and criteria exist (see, e.g., A. K. Ghosh (2006) and Peter Hall et al. (2008)). Heuristic values often do the job pretty well. A rule of thumb is that \(k=\sqrt{I}\) (\(I\) being the total number of instances) is not too far from the optimal value, unless \(I\) is exceedingly large.
Below, we illustrate this concept. We pick one date (31th of December 2006) and single out one asset (with stock_id equal to 13). We then seek to find the \(k=30\) stocks that are the closest to this asset at this particular date. We resort to the FNN package that proposes an efficient computation of Euclidean distances (and their ordering).
library(FNN) # Package for Fast Nearest Neighbors detection
knn_data <- filter(data_ml, date == "2006-12-31") # Dataset for k-NN exercise
knn_target <- filter(knn_data, stock_id == 13) %>% # Target observation
dplyr::select(features)
knn_sample <- filter(knn_data, stock_id != 13) %>% # All other observations
dplyr::select(features)
neighbors <- get.knnx(data = knn_sample, query = knn_target, k = 30)
neighbors$nn.index # Indices of the k nearest neighbors## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15]
## [1,] 905 876 730 548 1036 501 335 117 789 54 618 130 342 360 673
## [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25] [,26] [,27] [,28] [,29]
## [1,] 153 265 858 830 286 1150 166 946 192 340 162 951 376 785
## [,30]
## [1,] 2Once the neighbors and distances are known, we can compute a prediction for the return of the target stock. We use the function \(h(z)=e^{-z}\) for the weighting of instances (via the distances).
knn_labels <- knn_data[as.vector(neighbors$nn.index),] %>% # y values for neighb.
dplyr::select(R1M_Usd)
sum(knn_labels * exp(-neighbors$nn.dist) / sum(exp(-neighbors$nn.dist))) # Pred w. k(z)=e^(-z)## [1] 0.003042282## # A tibble: 1 × 1
## R1M_Usd
## <dbl>
## 1 0.089The prediction is neither very good, nor very bad (the sign is correct!). However, note that this example cannot be used for predictive purposes because we use data from 2006-12-31 to predict a return at the same date. In order to avoid the forward-looking bias, the knn_sample variable should be chosen from a prior point in time.
The above computations are fast (a handful of seconds at most), but hold for only one asset. In a \(k\)-NN exercise, each stock gets a customed prediction and the set of neighbors must be re-assessed each time. For \(N\) assets, \(N(N-1)/2\) distances must be evaluated. This is particularly costly in a backtest, especially when several parameters can be tested (the number of neighbors, \(k\), or \(a\) in the weighting function \(h(z)=e^{-az}\)). When the investment universe is small (when trading indices for instance), k-NN methods become computationally attractive (see for instance Y. Chen and Hao (2017)).