Agarwal, Amit, Elad Hazan, Satyen Kale, and Robert E Schapire. 2006. “Algorithms for Portfolio Management Based on the Newton Method.” In Proceedings of the 23rd International Conference on Machine Learning, 9–16. ACM.
Arjovsky, Martin, Léon Bottou, Ishaan Gulrajani, and David Lopez-Paz. 2019. “Invariant Risk Minimization.” arXiv Preprint, no. 1907.02893.
Aronow, Peter M., and Fredrik Sävje. 2019. “Book Review. The Book of Why: The New Science of Cause and Effect.” Journal of the American Statistical Association 115 (529): 482–85.
Barberis, Nicholas, Robin Greenwood, Lawrence Jin, and Andrei Shleifer. 2015. “X-CAPM: An Extrapolative Capital Asset Pricing Model.” Journal of Financial Economics 115 (1): 1–24.
Basak, Jayanta. 2004. “Online Adaptive Decision Trees.” Neural Computation 16 (9): 1959–81.
Beery, Sara, Grant Van Horn, and Pietro Perona. 2018. “Recognition in Terra Incognita.” In Proceedings of the European Conference on Computer Vision (Eccv), 456–73.
Ben-David, Shai, John Blitzer, Koby Crammer, Alex Kulesza, Fernando Pereira, and Jennifer Wortman Vaughan. 2010. “A Theory of Learning from Different Domains.” Machine Learning 79 (1-2): 151–75.
Blum, Avrim, and Adam Kalai. 1999. “Universal Portfolios with and Without Transaction Costs.” Machine Learning 35 (3): 193–205.
Brodersen, Kay H, Fabian Gallusser, Jim Koehler, Nicolas Remy, Steven L Scott, and others. 2015. “Inferring Causal Impact Using Bayesian Structural Time-Series Models.” Annals of Applied Statistics 9 (1): 247–74.
Bühlmann, Peter, Jonas Peters, Jan Ernest, and others. 2014. “CAM: Causal Additive Models, High-Dimensional Order Search and Penalized Regression.” Annals of Statistics 42 (6): 2526–56.
Chow, Ying-Foon, John A Cotsomitis, and Andy CC Kwan. 2002. “Multivariate Cointegration and Causality Tests of Wagner’s Hypothesis: Evidence from the UK.” Applied Economics 34 (13): 1671–7.
Cont, Rama. 2007. “Volatility Clustering in Financial Markets: Empirical Facts and Agent-Based Models.” In Long Memory in Economics, 289–309. Springer.
Coqueret, Guillaume. 2020. “Stock Specific Sentiment and Return Predictability.” Quantitative Finance Forthcoming.
Coqueret, Guillaume, and Tony Guida. 2020. “Training Trees on Tails with Applications to Portfolio Choice.” Annals of Operations Research 288: 181–221.
Cornuejols, Antoine, Laurent Miclet, and Vincent Barra. 2018. Apprentissage Artificiel: Deep Learning, Concepts et Algorithmes. Eyrolles.
Cover, Thomas M. 1991. “Universal Portfolios.” Mathematical Finance 1 (1): 1–29.
Cover, Thomas M, and Erik Ordentlich. 1996. “Universal Portfolios with Side Information.” IEEE Transactions on Information Theory 42 (2): 348–63.
Crammer, Koby, Ofer Dekel, Joseph Keshet, Shai Shalev-Shwartz, and Yoram Singer. 2006. “Online Passive-Aggressive Algorithms.” Journal of Machine Learning Research 7 (Mar): 551–85.
Engle, Robert F. 1982. “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation.” Econometrica, 987–1007.
Granger, Clive WJ. 1969. “Investigating Causal Relations by Econometric Models and Cross-Spectral Methods.” Econometrica, 424–38.
Hahn, P Richard, Jared S Murray, and Carlos Carvalho. 2019. “Bayesian Regression Tree Models for Causal Inference: Regularization, Confounding, and Heterogeneous Effects.” arXiv Preprint, no. 1706.09523.
Hazan, Elad, Amit Agarwal, and Satyen Kale. 2007. “Logarithmic Regret Algorithms for Online Convex Optimization.” Machine Learning 69 (2-3): 169–92.
Hazan, Elad, and others. 2016. “Introduction to Online Convex Optimization.” Foundations and Trends in Optimization 2 (3-4): 157–325.
Heinze-Deml, Christina, Jonas Peters, and Nicolai Meinshausen. 2018. “Invariant Causal Prediction for Nonlinear Models.” Journal of Causal Inference 6 (2).
Hiemstra, Craig, and Jonathan D Jones. 1994. “Testing for Linear and Nonlinear Granger Causality in the Stock Price-Volume Relation.” Journal of Finance 49 (5): 1639–64.
Hoi, Steven CH, Doyen Sahoo, Jing Lu, and Peilin Zhao. 2018. “Online Learning: A Comprehensive Survey.” arXiv Preprint, no. 1802.02871.
Hünermund, Paul, and Elias Bareinboim. 2019. “Causal Inference and Data-Fusion in Econometrics.” arXiv Preprint, no. 1912.09104.
Kalisch, Markus, Martin Mächler, Diego Colombo, Marloes H Maathuis, Peter Bühlmann, and others. 2012. “Causal Inference Using Graphical Models with the R Package Pcalg.” Journal of Statistical Software 47 (11): 1–26.
Khedmati, Majid, and Pejman Azin. 2020. “An Online Portfolio Selection Algorithm Using Clustering Approaches and Considering Transaction Costs.” Expert Systems with Applications Forthcoming: 113546.
Koshiyama, Adriano, Sebastian Flennerhag, Stefano B Blumberg, Nick Firoozye, and Philip Treleaven. 2020. “QuantNet: Transferring Learning Across Systematic Trading Strategies.” arXiv Preprint, no. 2004.03445.
Li, Bin, and Steven CH Hoi. 2014. “Online Portfolio Selection: A Survey.” ACM Computing Surveys (CSUR) 46 (3): 35.
Li, Bin, and Steven Chu Hong Hoi. 2018. Online Portfolio Selection: Principles and Algorithms. CRC Press.
Maathuis, Marloes, Mathias Drton, Steffen Lauritzen, and Martin Wainwright. 2018. Handbook of Graphical Models. CRC Press.
Pan, Sinno Jialin, and Qiang Yang. 2009. “A Survey on Transfer Learning.” IEEE Transactions on Knowledge and Data Engineering 22 (10): 1345–59.
Pearl, Judea. 2009. Causality: Models, Reasoning and Inference. Second Edition. Vol. 29. Cambridge University Press.
Peters, Jonas, Dominik Janzing, and Bernhard Schölkopf. 2017. Elements of Causal Inference: Foundations and Learning Algorithms. MIT Press.
Quionero-Candela, Joaquin, Masashi Sugiyama, Anton Schwaighofer, and Neil D Lawrence. 2009. Dataset Shift in Machine Learning. MIT Press.
Regenstein, Jonathan K. 2018. Reproducible Finance with R: Code Flows and Shiny Apps for Portfolio Analysis. Chapman & Hall / CRC.
Spirtes, Peter, Clark N Glymour, Richard Scheines, and David Heckerman. 2000. Causation, Prediction, and Search. MIT Press.
Tikka, Santtu, and Juha Karvanen. 2017. “Identifying Causal Effects with the R Package Causaleffect.” Journal of Statistical Software 76 (1): 1–30.
Weiss, Karl, Taghi M Khoshgoftaar, and DingDing Wang. 2016. “A Survey of Transfer Learning.” Journal of Big Data 3 (1): 9.
Widrow, Bernard, and Marcian E Hoff. 1960. “Adaptive Switching Circuits.” In IRE Wescon Convention Record, 4:96–104.
Wong, Steven YK, Jennifer Chan, Lamiae Azizi, and Richard YD Xu. 2020. “Time-Varying Neural Network for Stock Return Prediction.” arXiv Preprint, no. 2003.02515.
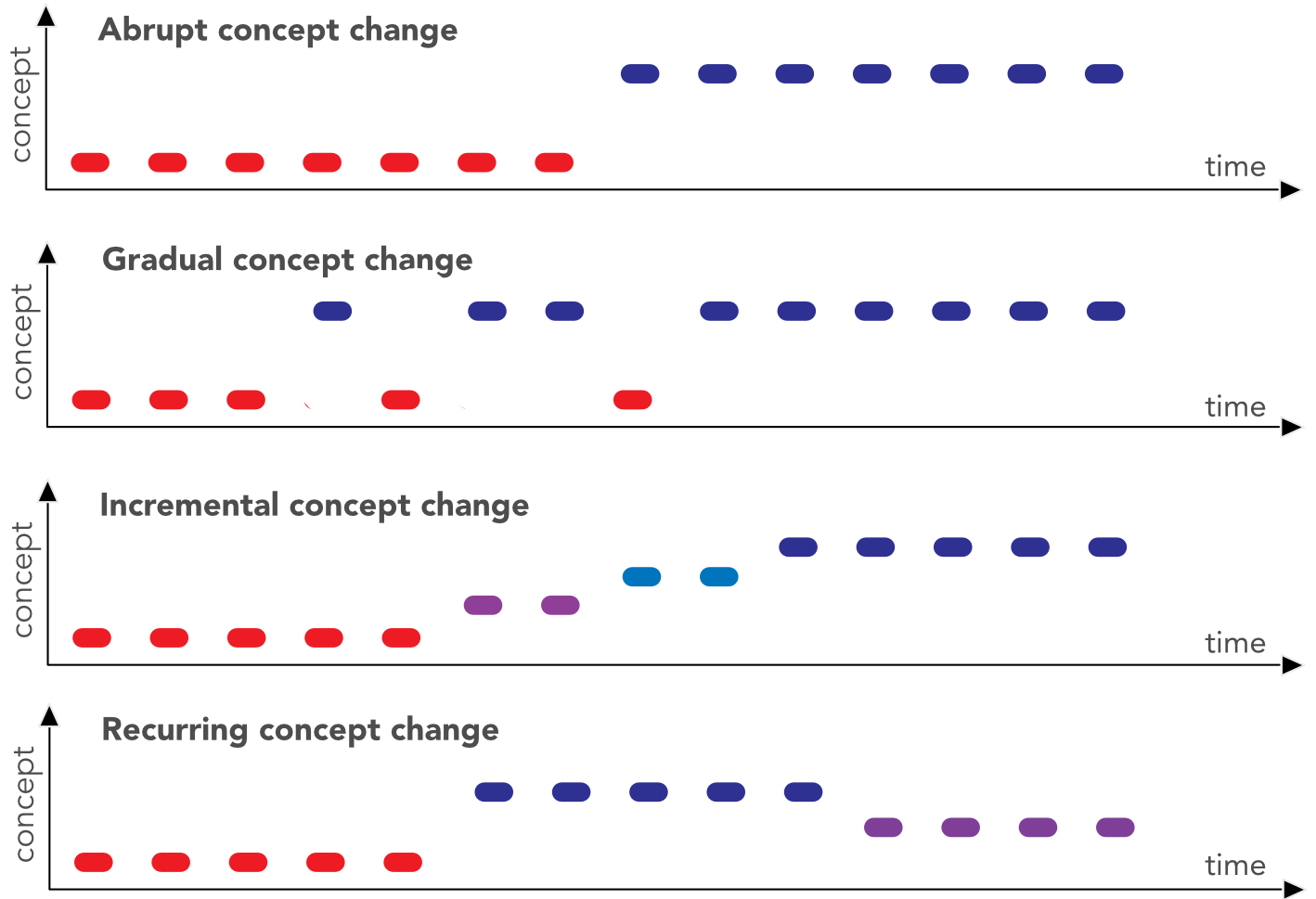 FIGURE 14.3: Different flavors of concept change.
FIGURE 14.3: Different flavors of concept change.