Belle, Vaishak, and Ioannis Papantonis. 2020. “Principles and Practice of Explainable Machine Learning.” arXiv Preprint, no. 2009.11698.
Chen, Jianbo, Le Song, Martin J Wainwright, and Michael I Jordan. 2018. “L-Shapley and c-Shapley: Efficient Model Interpretation for Structured Data.” arXiv Preprint, no. 1808.02610.
Fisher, Aaron, Cynthia Rudin, and Francesca Dominici. 2019. “All Models Are Wrong, but Many Are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously.” Journal of Machine Learning Research 20 (177): 1–81.
Friedman, Jerome H. 2001. “Greedy Function Approximation: A Gradient Boosting Machine.” Annals of Statistics, 1189–1232.
Gower, John C. 1971. “A General Coefficient of Similarity and Some of Its Properties.” Biometrics, 857–71.
Hall, Patrick, and Navdeep Gill. 2019. An Introduction to Machine Learning Interpretability - Second Edition. O’Reilly.
Lundberg, Scott M, and Su-In Lee. 2017. “A Unified Approach to Interpreting Model Predictions.” In Advances in Neural Information Processing Systems, 4765–74.
Molnar, Christoph. 2019. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable. LeanPub / Lulu.
Molnar, Christoph, Giuseppe Casalicchio, and Bernd Bischl. 2018. “Iml: An R Package for Interpretable Machine Learning.” Journal of Open Source Software 3 (27): 786.
Ribeiro, Marco Tulio, Sameer Singh, and Carlos Guestrin. 2016. “Why Should I Trust You?: Explaining the Predictions of Any Classifier.” In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, 1135–44. ACM.
Shapley, Lloyd S. 1953. “A Value for N-Person Games.” Contributions to the Theory of Games 2 (28): 307–17.
Staniak, Mateusz, and Przemyslaw Biecek. 2018. “Explanations of Model Predictions with Live and breakDown Packages.” arXiv Preprint, no. 1804.01955.
Vidal, Thibaut, Toni Pacheco, and Maximilian Schiffer. 2020. “Born-Again Tree Ensembles.” arXiv Preprint, no. 2003.11132.
Zhao, Qingyuan, and Trevor Hastie. 2020. “Causal Interpretations of Black-Box Models.” Journal of Business & Economic Statistics Forthcoming.
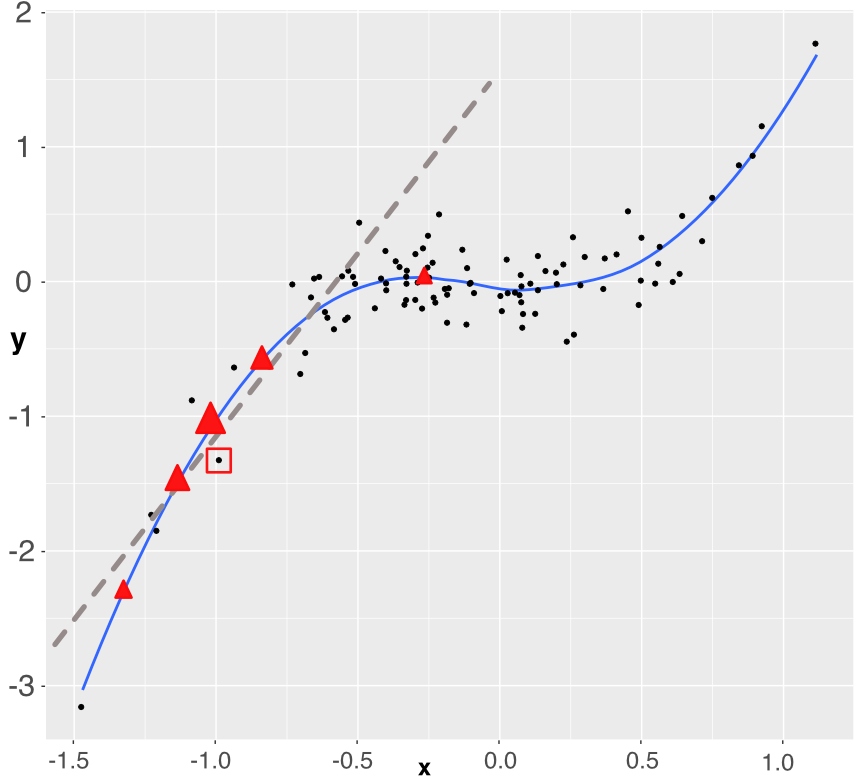 FIGURE 13.5: Simplistic explanation of LIME: the explained instance is surrounded by a red square. Five points are generated (the triangles) and a weighted linear model is fitted accordingly (dashed grey line).
FIGURE 13.5: Simplistic explanation of LIME: the explained instance is surrounded by a red square. Five points are generated (the triangles) and a weighted linear model is fitted accordingly (dashed grey line).